Ngẫu nhiên là gì?

Ngẫu nhiên (randomness), một ý tưởng nền móng cho sự phát triển của khoa học, được định nghĩa trên wiki như sau:

Và nó hoàn toàn đúng. Loài người đã từ chỗ không biết gì đến sự ngẫu nhiên, cho đến khi lợi dụng được nó để phát triển vượt bậc.

Đầu óc chúng ta không được thiết kế để có cái gọi là giác quan (intuition) về sự ngẫu nhiên, mặc dù nó xảy ra liên tục trong cuộc sống của mỗi người. Vì thực ra ý tưởng này mới được khái quát bằng toán gần đây (từ thế kỷ 16), nên điều này hoàn toàn có thể hiểu được.

Nếu toán là logic cho sự chắc chắn (certainty), thì xác xuất là logic cho sự bất định (uncertainty).

Nghĩa là sao?

So sánh

Toán được xây dựng trên cơ sở các số nguyên, ví dụ 1, 2, 3, 4 ... nghĩa là đếm được. Vì đấy là cách sớm nhất là nguyên thủy nhất con người được làm quen với toán.

Sau đó ta đặt các biến, ví dụ như

$x = 1 \\ y = 2 \\ z = x + y$

Toán dần dần tách biệt ra khỏi các con số. Nó bắt đầu dựa vào logic nhiều hơn. Vì nếu ta có thể chứng minh được một định lý là đúng theo logic, thì nó sẽ luôn đúng trong mọi trường hợp.

Với xác suất, ta cũng có thể đặt biến cho một sự việc ngẫu nhiên, gọi là biến ngẫu nhiên (random variable)

$X = \text{sáng ngày 27/6/2022 có mưa từ 9 đến 12 giờ} \\ Y = \text{quay xúc sắc ra được mặt 6} \\$

Với mỗi biến trên, thay vì có kết quả là số, ta sẽ có kết quả là một xác suất sự việc đấy xảy ra, có thể từ 0 (không thể xảy ra) đến 1 (chắc chắn xảy ra)

Với xác suất cổ điển, khi coi mọi thứ có khả năng xảy ra là như nhau, thì việc tính toán khá dễ dàng nhưng không thực tế.

Vì sao? Vì trên thực tế có quá nhiều yếu tố ảnh hưởng lẫn nhau, và khi có quá nhiều biến số, mỗi biến lại ảnh hưởng đến nhau theo một kiểu khác nhau thì tính toán được là điều không thể.

Bayes Theorem

Như đã nói trên, xác suất cổ điển là không thực tiễn. Những bộ óc vĩ đại như Newton cũng còn phạm sai lầm khi dính đến xác suất.

Vào thế kỷ 17, một nhà thống kê học tên Thomas Bayes đã tìm ra được một định lý, mà định lý đó hiện giờ là hòn đá nền móng cho xác suất thống kê hiện đại.

Nói đơn giản ra thì ông tìm được bản chất của xác suất. Nếu bạn muốn tìm hiểu thêm thì mua quyển How not to be wrong đọc nhé.

Khi chúng ta hiểu được về xác suất, khoa học đã tiến bộ nhanh không tưởng.

Vì khi chúng ta hi sinh một chút sự chính xác, thì sự thật bắt đầu dần được tiết lộ.

Quy luật và sự tương quan

Toán và xác suất giống nhau ở 1 chỗ, đó là nhằm tìm ra các quy luật và mối tương quan của vạn vật.

Các quy luật đó được viết lại dưới dạng các ký tự toán học, để có thể truyền đạt được ý tưởng nhanh nhất và chính xác nhất có thể.

Ví dụ như Euler Formula, một phương trình nhìn qua tưởng chừng đơn giản, nhưng đã hợp nhất được 4 lĩnh vực: đại số, lượng giác, số phức, và tích phân.

$e^{ix} = cos(x) + i sin(x)$

Với $x=\pi$, ta có Euler Identity

$e^{i\pi} = -1$

Với $x=\tau=2\pi$

$e^{i\pi} = 1$

From Chapter 22 of The Feynman Lectures on Physics, Volume I:

"We summarize with this, the most remarkable formula in mathematics: $e^{i\theta} = cos(\theta) + i sin(\theta)$.
This is our jewel.
We may relate the geometry to the algebra by representing complex numbers in a plane; the horizontal position of a point is $x$, the vertical position of a point is $y$.
We represent every complex number, $x + iy$. Then if the radial distance to this point is called $r$ and the angle is called $\theta$, the algebraic law is that $x + iy$ is written in the form $r e^{i\theta}$, where the geometrical relationships between $\text{x, y, r, and }\theta$ are as shown. This, then, is the unification of algebra and geometry."

Còn xác suất thì sao?

Bayes Modeling và Model Inference

Xác suất khác với toán ở chỗ, nó ko có một con số cụ thể cho bạn, mà chỉ cho bạn biết được một thứ gọi là phân phối (distribution). Dùng phân phối này bạn có thể tìm ra được quy luật giữa các dữ liệu đầu vào.

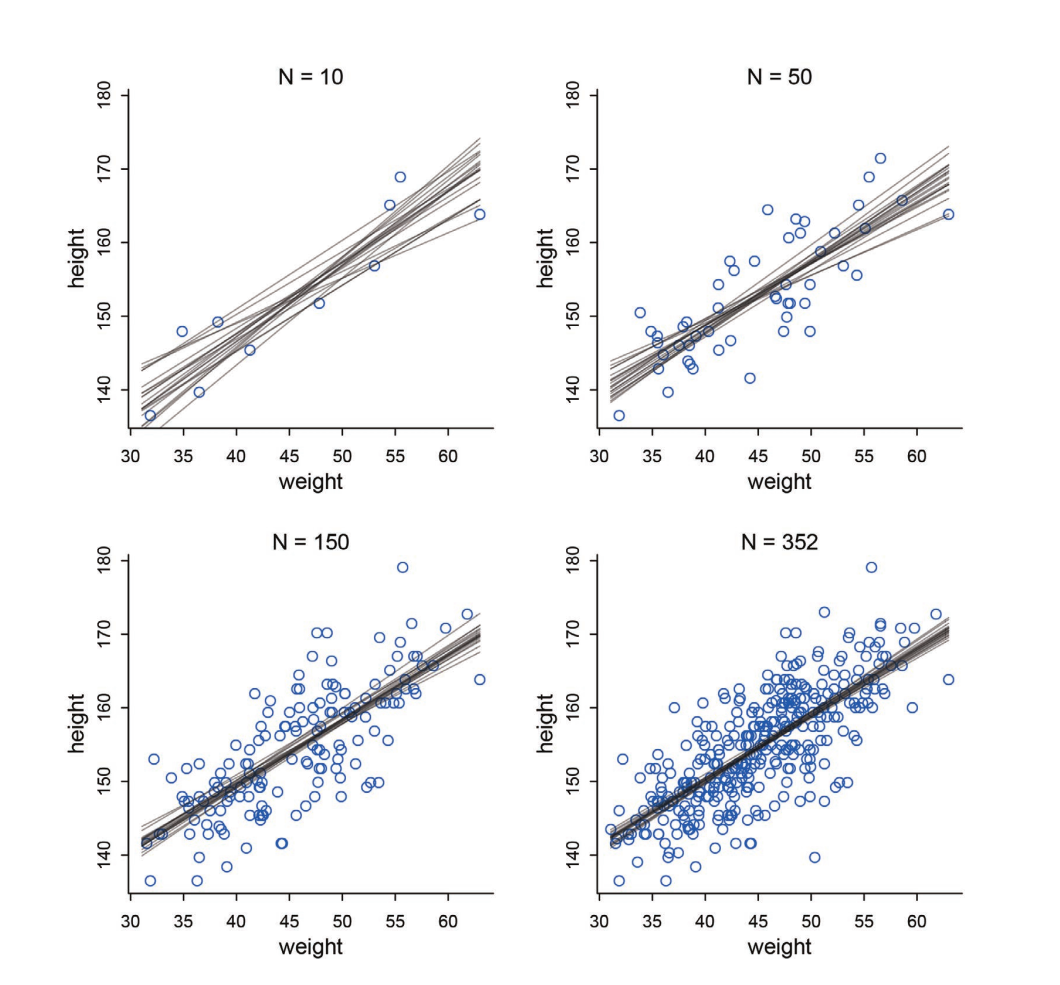
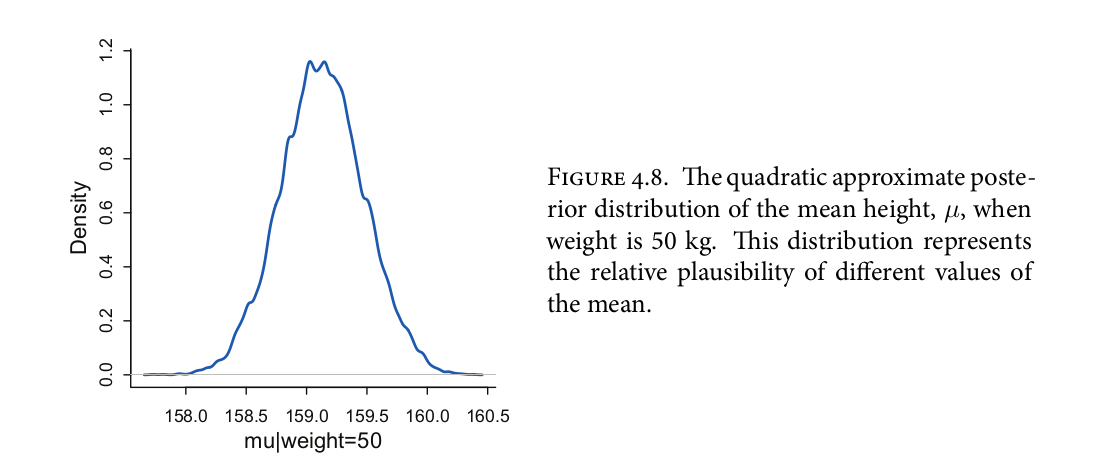
Ví dụ như, hút thuốc lá có tăng tỷ lệ ung thư không? Bạn đi tìm ngẫu nhiên 100 người trên 18 tuổi, rồi tạo 1 bảng gồm 2 cột, 1 cột là có hút thuốc trên 1 năm hay ko, cột còn lại là có ung thư hay không. Sau khi tạo model và có kết quả, ta có thể xem được có mối tương quan hay không và có thể đưa ra hành động phù hợp.

Đây là bước khởi đầu cho khoa học đích thực, sự hỗn loạn được công thức hóa, và con người có thể kiểm chứng nhiều giả thuyết của mình chính xác hơn.

Kỷ nguyên mới

Vấn đề bắt đầu khi bạn có quá nhiều dữ liệu. Nhưng giỏi ứng biến, những người khai phá internet thời đầu đã bắt đầu manh nha biến đống dữ liệu đấy thành mỏ vàng.

May mắn theo định luật Moore, công nghệ phát triển theo cấp số nhân, các thuật toán dùng để phân tích và dự đoán được đưa vào sử dụng để tìm ra quy luật.

Và điều kỳ diệu bắt đầu xuất hiện. Những tác vụ đơn giản như nhận diện hình ảnh, tưởng chừng như không thể

thì giờ dùng điện thoại cũng có thể làm được.

Cả một kỷ nguyên mới được mở ra cho nhân loại, nhờ lợi dụng được sự ngẫu nhiên. Nhưng, họ đã làm như thế nào?

Machine Learning & Deep Learning

<Đón xem phần 2>